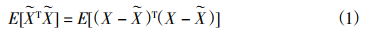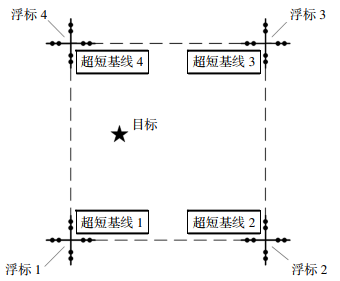
水下運動目標位置是海洋調查、工程探測、海上實驗等科研活動的重要參數，特別是在海上靶場的裝備試驗中，需要實時精確地獲得水下運動目標的位置信息。水聲定位技術是獲得這一信息的有效手段，近年來，水聲定位技術不斷發展，水聲定位系統也由傳統的長基線系統 （Long Baseline System，LBL）、短基線系統 （Short Baseline System，SBL）、超短基線系統 （Ultra-short Baseline System，USBL）向聲學多基線組合與慣導、GPS（Global PositioningSystem） 等聯合定位的模式轉變。相關研究表明[1-4]，長基線具有基線長、定位精度高的特點，但是長基線定位是以精確時延進行測量，對由于目標運動使得同步信標需要高幀率發射所帶來的抗距離模糊解算能力不強；超短基線定位系統則是由多元聲基陣與聲信標組成，通過測量距離和方位定位，其優點是尺寸小、使用方便，其方位參量的測量不受距離模糊的影響，缺點是跟蹤數據不連續，無法連續跟蹤水下目標的運動軌跡，且其定位精度受到載體安裝形變誤差、位姿組件測量誤差和聲速誤差等因素影響，每次安裝后需進行校準，系統定位精度不高，僅適用于大范圍作業區域跟蹤 [5]。鑒于此，本文提出一種采用浮標方式基于長基線交匯的超短基線定位技術實現對水下低速運動目標的高精度定位測量。

1 系統組成及關鍵技術
      目前，組合式水聲定位系統在國內得到了廣泛應用。中科院聲學所東海研究站等單位[6]研究了一種長基線和超短基線組合的定位方式實現對水下拖曳目標定位，但是在使用中需要采用多艘艦船配合使用，超短基線安裝于船體易受到船舶噪聲干擾影響檢測，特別是系統使用前每次需進行超短基線陣與慣性組件安裝誤校準，一方面造成測量保障實施難度較大，另一方面也帶來不應有的測量誤差，降低了定位精度。本文涉及的定位系統采用長基線和超短基線組合定位，利用海洋浮標技術將兩者組合，可有效地避免前述不足，特別是降低了系統受到本船的噪聲干擾，提升超短基線的方位檢測能力，利用長基線對目標的精確時延測距，基于時延/相位差參量融合的組合定位，不僅彌補了單一定位方式的定位精度局限性，而且能夠在布放較少定位基元的情況下，提供較高的定位精度，有利于系統使用和拓展[7]。

1.1 系統組成
      本系統由浮標式水聲定位測量分系統、顯示控制分系統組成，可完成靶場海上試驗水下低速目標定位測量、試驗指揮及態勢顯示等任務。浮標式水聲定位測量分系統由浮標式長基線水聲測量分機、水聲測量處理分機、水聲同步信標及水聲指令機等組成。浮標式長基線水聲測量分機由浮標、水聲長基線測距機、超短基線基陣、方位姿態慣性組件、高精度北斗差分接收機、無線數傳機等組成，由多個安裝有超短基線陣的浮標構成長基線測量陣，對加裝了水聲同步信標的水下運動目標進行定位，浮標測量信息通過無線鏈路傳至測量船水聲測量處理分機解算出水下目標位置。

1.2 系統關鍵技術

      為滿足對水下運動目標的連續定位，同時也為了克服船載超短基線定位使用上的不足，系統采用了浮標方式，浮標采用了高浮力低重心的結構設計，經抗沖擊結構設計后，可以滿足爆炸試驗抗沖擊要求；同步式信標安裝于水下航行體或運動爆源上，為滿足不同速度運動目標的測量需要，水聲同步信標采用了信號發射周期可調 （0.5~5 s） 的高增益寬帶多址調頻雙脈沖信號體制，相比分頻段的線性調頻或跳頻信號可獲得更大的處理增益，在相同作用距離下，可降低發射聲源級，減小系統的功耗，提高系統靈敏度，提高定位精度。其系統設計中所涉及的關鍵技術如下。

（1） 基于長基線和超短基線數據融合的定位

       長基線與超短基線結合使用可以構成組合聲學定位系統，組合定位系統通常可以獲得目標信號的多種特征參量，合理地融合多參量信息有利于提高定位系統的精度及可靠性。考慮到長基線定位系統作用范圍廣且陣內定位精度較高，超短基線定位系統集成度高且具備良好的近程定位優勢，本文構建了基于長基線交匯的超短基線定位系統，并采用合作信標模式對其進行廣域精確可靠定位，系統各個節點均由十字型超短基線陣構成。提出時延/相位差參量融合組合基線信息融合定位方法，通過基于最小均方誤差和最大似然估計準則下的定位優化模型有效融合兩種參量的觀測信息，以實現對整個測量區域的高精度定位。

（2） 高同步速率下的運動目標定位抗距離模糊技術

      對水下運動目標進行定位時，為了獲得足夠的軌跡采樣點數來描繪其運動過程，定位系統需要采用較短的同步周期。聲速和系統同步周期的乘積稱為最大非模糊距離，以信號發射周期為 0.2 s為例，若聲速取 1 500 m/s，則系統最大非模糊距離為300 m。當目標距離定位陣元超過 300 m時，信號傳播時延大于 0.2 s，而接收系統記錄的時延值仍在0.2 s以內，即時延測量值與真實的時延值相差周期的整數倍，相應地，距離估計值與實際值相差最大非模糊距離的整數倍，稱為距離模糊問題，該倍數稱為模糊周期數，求解模糊周期數以獲得實際距離估計值稱為解距離模糊。距離模糊問題直接導致運動目標定位結果具有多值性。

針對上述問題，考慮到方位參量的測量不受距離模糊的影響，采用最大似然準則下時延/方位融合定位優化模型，將解距離模糊問題轉化為方位參量約束條件下非線性優化問題，并采用差分進化算法求解。利用方位信息對目標所在區域進行限定，降低了差分進化算法陷入局部最優解的危險。無需目標初始就位點，即可實現對大范圍測量區域內運動目標的無模糊定位。

（3） 淺海復雜環境下精確時延估計
      由超短基線定位原理可知，水聲定位測量分機的相位測量主要是依靠測量聲基陣陣元間的相位差來完成的，其本質是時延差的測量，精確測量時延差的前提是精確測量每個陣元的時延。一般來講，對于單頻信號大多采用能量檢測方式對信號進行時延估計；調頻信號則大多采用拷貝相干方式對信號進行前沿檢測。淺海水聲信道是更為復雜的多途相干信道，經多徑傳輸到達接收端的信號與發射波形有顯著不同，且隨著相對距離的變化，直達聲和反射聲不斷改變。信號反向疊加導致疊加部分的信號幅度非常小，因此接收機前端的信號呈現“邊沿”現象。這樣就容易導致直達聲漏報，使得系統檢測時延值出現大幅度跳變。對于聲基陣來說，若各陣元的有效脈沖時延值隨機跳變，將嚴重影響系統定位精度。系統利用初測+精測的手段，對接收的信號采取二次時延估計，使各通道間的時延測量精度保證在 1 滋s，可以很好地解決淺海復雜環境下精確時延估計。

（4） 浮標方式下超短基線基陣誤差的減小與消除

      超短基線陣是利用相位差進行定位的，聲基陣的設計和校準直接影響信號間的相位差。聲基陣陣元間的初始相位及安裝位置偏差是直接影響定位精度的關鍵因素。聲基陣陣元間的初始相位會直接帶來相位測量誤差，屬于系統誤差，需要出廠前在消聲水池或開闊水域進行校準獲得，然后修正到基陣測量的相位差，以減少對整個系統定位精度的影響；聲基陣坐標與大地坐標間的旋轉角度誤差很難直接測量，此誤差主要由安裝誤差引起，可通過文獻[8]介紹的方法進行校準，系統采用浮標方式，超短基線陣固定安裝浮標下部，經過一次校準即可，避免船載基陣每次安裝后均需進行適應性校準，試驗效率低的弊端。
2 系統信息融合定位算法研究
長基線和超短基線組合定位模型如圖 2所示。

圖 2長基線和超短基線組合定位模型
長基線和超短基線的工作是相互獨立的，根據上述模型，按照下列準則獲取測量信息。
（1） 當有效浮標 （長基線基元） 個數足夠多時（不小于 3），定位模型以長基線為主，超短基線提供相位差參量信息主要用于抗距離模糊，對冗余陣元測距信息進行融合加權處理；

（2） 當使用兩個浮標，采用長基線方式求解，超短基線利用相位差參量信息判斷雙解；

（3） 當單浮標接收目標信號時，直接利用超短基線求解，根據已測得歷史位置信息判別真解，提出模糊解；
（4） 對于超短基線的相位模糊問題，則在基陣設計中通過優化設計解決，采用小于半波長的兩陣元相位信息實現相位的解卷積，剔除相位模糊解。

      本文假設兩個系統同時工作，一共能得到 5組定位結果，包括 1組長基線結果和 4組超短基線定位結果。定位結果融合的關鍵是如何將 5組信息進行有效的組合，使融合的定位結果優于單個系統的定位結果。

2.1 最小均方誤差估計與最大似然估計
      數理統計中均方誤差是指參數估計值與真值之差平方的期望值，記為 MSE，是衡量“平均誤差”的一種較為方便的方法，可以評價數據的變化程度，均方誤差值越小，說明預測模型描述的結果精確度越高。

      在已知 X和 Z是兩個隨機矢量，且二者存在聯合概率密度函數的條件下，使各估計分量的均方誤差之和最小的估計，被稱為最小均方誤差估計X贊 V。各估計分量的均方誤差之和可以表示如下。

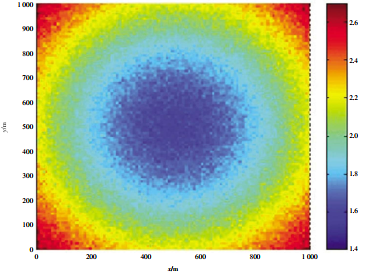
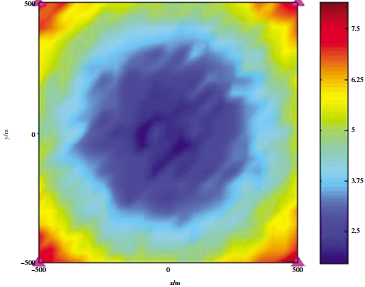
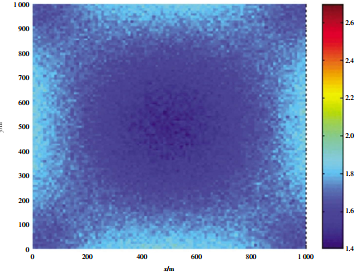
      最大似然估計是建立在最大似然原理基礎上的一個統計方法，是概率論在數理統計中的一個應用。最大似然估計提供了一種“模型已定，參數未知”的方法，通過若干次試驗，觀察其結果，利用試驗結果得到某個參數值能夠使樣本出現的概率為最大。

2.2 基于最小均方誤差準則的時延/相位差參量融合定位優化模型

      可知融合結果的定位精度不低于各系統單獨定位精度，基于最小均方誤差準則的融合方法是可行的。

2.3 最大似然準則下的時延/相位差參量融合定位優化模型

      時延/相位差參量融合組合基線定位方法是通過構建最大似然準則下的優化定位模型，有效融合兩種參量的觀測信息，以實現整個測量區域的高精度定位。

3 系統定位精度分析

      為了驗證組合定位測量的定位精度，本文分別對長基線、超短基線和長基線/超短基線組合定位的定位精度進行仿真，并在組合定位方式下分別對基于最小均方誤差準則和最大似然準則這兩種時延/相位差參量融合算法進行仿真。具體仿真條件如下。

（1） 浮標 （陣元） 位置精度 （北斗/GPS定位精度：3 m）；
（2） 聲速測量誤差為 2譯；
（3） 時延測量誤差為 200 滋s；
（4） 相位差測量誤差為 2.2毅；
（5） 超短基陣陣元間距 0.25 m，陣元安裝誤差為 0.6 mm；
（6） 蒙特卡洛統計次數為 2000次。

圖 3至圖 6分別為長基線、超短基線、組合定位下兩種融合算法的定位精度。

      由仿真結果可知，長基線的定位精度由于可以獲得精確的時延估計，對于位于陣中心的定位精度較高；超短基線遠距定位精度較低，但是局域定位精度較高，長基線/超短基線組合定位的定位精度在距離陣元較近位置比長基線要高，在較遠距離位置定位精度高于超短基線，采用兩種準則進行數據融合處理后的定位精度，在陣中心遠距精度幾乎相同，在距離陣元較近位置上基于最小均值誤差準則的組合定位精度較最大似然估計準則的要高。在總體上，采用組合定位方法可將長基線作用距離遠和超短基線局部區域精度高的優勢充分結合起來，這種方式的定位精度整體上要高于單一方式的定位精度。

     水下運動目標是具有一定速度的動態目標，其對信號檢測的影響體現在接收端接收到的信號具有多普勒效應，頻率會發生一定程度的偏移，導致時延檢測有偏差，仿真計算分析表明對于信號頻段20~30 kHz，脈寬 10 ms的水聲信號，在目標速度為

圖 3 長基線定位精度

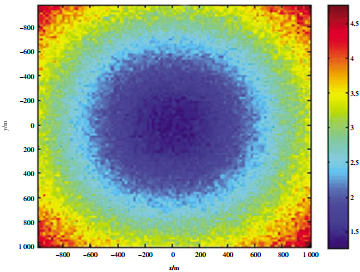
圖 4 超短基線定位精度

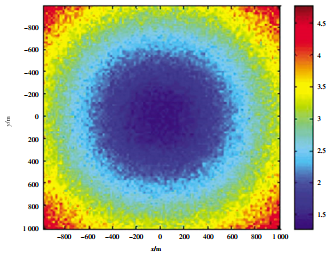
圖 5 基于最小均方誤差準則的組合定位精度

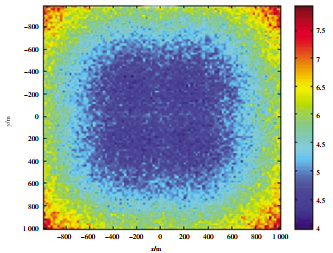
圖 6 基于最大似然估計準則的組合定位精度

       2 kn時，時延測量誤差約為 200 滋s；目標速度為4 kn時，時延測量誤差約為 400 滋s；目標速度為6 kn時，時延測量誤差約為 600 滋s；目標速度為8 kn時，時延測量誤差約為 800 滋s；據此，本文進一步仿真驗證了該組合定位方式下航速 0 kn的靜止目標 （圖 7） 和航速 8 kn下運動目標的定位精度（圖 8）。具體仿真條件為：除了航速 8 kn運動目標時延測量誤差為 800 滋s以外，其余仿真條件不變。

圖 7 水下靜止目標 （航速 0 kn） 的定位精度

圖 8水下低速運動目標 （航速 8 kn） 的定位精度

      仿真結果表明，在2km的作用范圍內，靜態目標水平定位精度不大于 2譯R（R為測量斜距），考慮動態目標的多普勒偏移及時延測量誤差，動態目標水平定位精度不大于 4譯R，可滿足系統的測量要求。

4 結 論

      本文提出一種基于浮標方式的長基線/超短基線組合定位系統實現對水下運動目標定位，采用浮標方式克服了船載超短基線組合安裝誤差大，避免安裝后每次均需進行姿態適應性校準的弊端，提高了測量精度；同時采用組合定位方式又可以有效減少長基線陣元數量，提高試驗效率。在組合定位解算中采用時延/相位差參量信息，依托基于最小均方誤差準則和最大似然估計準則的融合方法解決了同步信標高幀率、跨周期所帶來的距離模糊問題，提高了系統對運動目標的定位精度；文章最后仿真分析了各種方法的定位精度空間分布規律，驗證了這種定位方法要優于單個系統的定位精度。該方法無需每次試前都對基陣進行校準，具有使用效率高、試驗準備簡單、測量質效高等優點。目前，該系統已經在靶場得到成功應用。

班寧產品匯總