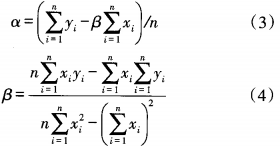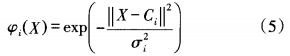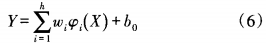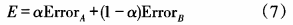|
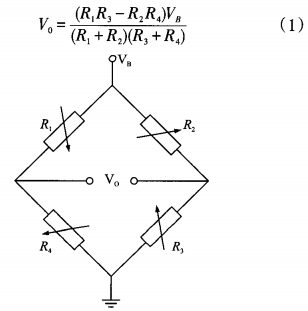
基于混合優化算法的壓力傳感器溫度補償 壓阻式壓力傳感器廣泛應用于各個領域,但是壓阻式壓力傳感器存在溫度漂移這一缺點, 由于其測量精度受溫度影響很大 , 因此不能夠在溫差變化范圍較大場合使用,這就制約了壓阻式壓力傳感器實用化進程的發展, 因此必須要對壓阻式壓力傳感器進行溫度補償,消除其對溫度的敏感程度。 專家學者對傳感器的溫度補償方法進行了深人研究:文獻中使用BP神經網絡建立溫度補償模型,并使用粒子群優化算法對BP神經網絡進行優化 ,避免 BP 神經網絡陷入局部最小值 ,提高補度。 文獻 [5 ] 中使用 RBF 神經 網絡建立溫度補型,并使用蟻群優化算法對 R BF 神經網絡進行優化,提高補償精度。 文獻[6]中使用基于遺傳模擬退火算法建立溫度補償模型。 文獻中提出的硬件電路改進方法,使用 M A X 1452 信號調理芯片對壓力傳感器進行溫度補償 ,實驗表明 ,此補償電路具有較好的補償效果 。 相比軟件方法的補償方法 ,該方法實現過程相對復雜 ,不易于對其他型號和種類傳感器移植。 1 壓力傳感器工作原理及溫度補償原理 溫度對壓力傳感器的影響主要體現在壓阻系數是與溫度有關的函數關系,壓阻系數會隨著溫度升高而降低 ,隨著溫度降低而升高。 其次 ,當環境溫度變化時會對傳感器產生附加的熱應力 ,由于擴散電阻具有不 同的熱膨脹系數 ,則會產生附件壓阻效應 。
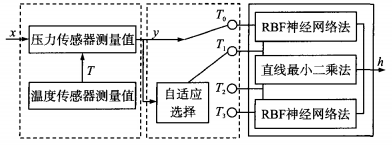
圖 1 壓阻式壓力傳感器工作原理 1.2 溫度補償原理 對傳感器進行為溫度補償原理如圖2所示 ,通常壓力傳感器在低溫段和高溫段 收到溫度影響較大, 因此在此階段使用補償性能較好, 但對系統要求較高的RBF神經網絡模型進行補償 ,而在中間段采用普通直線最小二乘法補償模型即可。通過設定溫度閥值實現不同補償模型之間的切換。
圖 2 壓力傳感器 溫度補償系統工作原理 2 直線最小二乘法補償模型 使用直線方程對傳感器進行溫度補償 : 式 中,O/為常數項 ; 為系數 ;e 為為擬合誤差。由文獻 [10 ]可知:
在使用直線擬合方程進行擬合時,為 了使得直線擬合的區間盡可能 的大 ,從而提高整體溫度補償方法的效率 ,降低計算復雜度 ,需要根據精度要求 ,自動搜尋 中間線性段的區間。 令初始 的區間為 [t ,t:] = [ t0,t ] ,對初始 區間進行直線擬合, 得到擬合誤差的最大值emax,若大于設定誤差下限,則令t1=t + π,其中為溫度值采樣間隔 ,對新生成的區間再次進行直線擬合 ,得到擬合誤差的最大值 e 若仍然大于設定誤差下限 ,則令 t2=t:一 ,對新生成的區間再次進行直線擬合 ,如此反復循環 ,直到得到擬合誤差的最大值 e 低于或等于設定誤差下限n 。 3 RBF神經網絡溫度補償模型 3.1 RBF神經網絡 RBF神經網絡通常由輸入層 、隱含層以及輸出層組成 ,隱含層輸出為 :
式中,為基函數的寬度;C為隱含節點中心。輸出層為 :
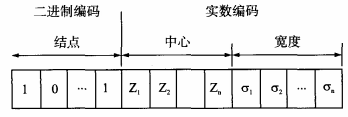
式中,W為隱含節點與輸出節點的連接權值 ;b0是輸出偏差。 RBF 神經網絡中 ,基函數的寬度、隱含節點中心Ci以及隱含節點與輸出節點的連接權值Wi是需要確定的基本參數 。 本文為提高常規RBF神經網絡泛化能力,采用混合優化算法獲取最優RBF神經網絡 的基函數的寬度、隱含節點中心G以及輸出節點的連接權值值,發揮進化算法優秀的全局搜索能力以及梯度下降算法優秀的局部搜索能力 ,進而提高傳感器非線性段溫度補償效果 。 具體方法如下 : 圖3 混合編碼結構 之后使用訓練樣本對神經網絡進行訓練,如果滿足終止條件,則停止優化,所帶參數即為最優網絡參數,并建立溫度補償模型。 如果不滿足終止條件 ,則使用加權適應度 函數進行個體適應度值計算 。 常規 R B F 神經網絡使用進化算法進行優化時 ,采用的適應度函數為訓練樣本的誤差 , 這樣做法帶來 的過度擬合現象會導致訓練時誤差很小 ,而測試時的誤差依然較大。 解決問題的方法之一是使用加權誤差共 同作為適應度函數 :
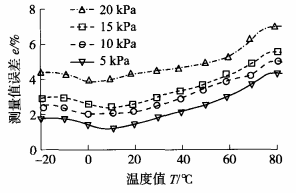
然后 ,為提高 了算法局部搜索能力 ,對進化后的新種群 中精英個體使用梯度下降算法迭代搜索 ,其概率為 P 。 對于不進行梯度下降算法的個體進行單形交叉操作 和均勻變異操作 。 進行單形交叉操作能夠使得優化算法在進化前期 和后期分別具有良好的全局優化能力和局部優化能力。 進行均勻變異操作能夠使得種群多樣性提高 ,從而避免早熟現象地發生。 最后繼續使用訓練樣本對神經 網絡進行訓練 ,循環上述優化過程 ,直至滿足終止條件 。 4 實驗研究 通過實驗方法對基于混合優化算法的壓力傳感器溫度補償方法進行實驗驗證 。 將壓力傳感器放置于一20 ℃~80 ℃溫度環境下 ,溫度每次變化10度 ,并保證恒溫環境 ,對傳感器分別施加 5 kPa,55 kPa壓力 ,每次變化5kPa。不同溫度下的標定 傳感器壓力值測量值與實際壓力值進行比較,得到測量誤差,并將誤差繪制成曲線如圖4所示。
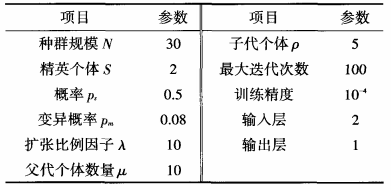
可以看出,在-20 ℃~10 ℃ 的低溫段以及55 ℃~80 ℃的高溫段 ,傳感器誤差變化呈現非線性 ,而在1O℃~ 55℃溫度區間內,傳感器誤差呈現線性變化。 因此在在10 ℃~55 ℃溫度區間內使用直線最小二乘法進行擬合,在兩端使用混合優化RBF神經網絡溫度補償模型 ,參數設定如表1所示 。
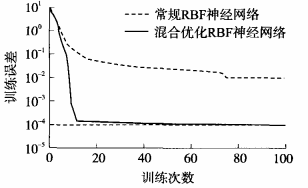
表1 RBF神經網絡溫度補償模型參數 使用常規RBF神經網絡與混合優化神經網絡進行比較研究,訓練誤差變化曲線如圖5所示。
圖5 訓練曲線 經過100次訓練迭代后,混合優化R BF神經網絡的訓練精度達到1.12 1x 10-4,常規 R B F 神經網絡的訓練精度為 1.657 ×10-2。 可以看出, 混合優化RBF神經網絡比較常規RBF神經網絡具有更高的訓練精度和訓練效率。 分別使用4種方法對壓力傳感器在5kPa~55 kPa 壓力范圍以及-2O ℃~80 ℃溫度范圍內進行溫度補償 :
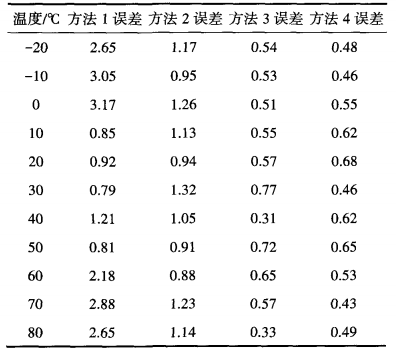
表2 溫度補償方法作用下傳感器測量誤差單位:% 表 2 中各溫度值對應的數據為使用該種溫度補償方法時 ,5kPa~55 kPa 各個壓力點下的誤差平均值 。 在一20 ℃~80 ℃溫度范圍內,使用溫度補償方法 1 的平均誤差為 1.92 %,使用溫度補償方法 2 的平均誤差為 1.09% ,使用溫度補償方法3的平均誤差為0.55% ,使用溫度補償方法4的平均誤差為0 .5 3%。 在-20 ℃~80 ℃溫度 內均使用直線最小二乘法溫度補償模型, 在10 ℃~55 cC溫度 內直線最小二乘法 溫度 補償模 型顯現 了較 好 的補償 效果 ,誤 差在1%以下 ,但是在兩端低溫和高端區域,誤差較大,在2%~3%之間 。 在-20 ℃~80 ℃溫度 內均使用常規RBF 神經網絡溫度補償模型 ,顯現 了 R BF 神經網絡溫度補償模型較好 的擬合效果 ,誤差控制在 1%左右。 在-20 ℃ ~80 ℃溫度內均使用混合優化RBF神經網絡溫度補償模型 ,顯現 了本文使用的混合優化算法對 RB F 神經網絡溫度補償模型的優化性能,誤差控制在 l%以內。 5 結論 ②在各溫度范圍內均使用RBF神經 網絡溫度補償模型時,顯現了RBF神經網絡溫度補償模型較好的擬合效果。 ③使用混合優化算法優化RBF神經網絡溫度補償模型后,使得補償效果有所提升。 ④在 中間溫度范圍使用直線最小二乘法溫度補償模型,在兩端低溫和高端區域內使用混合優化RBF神經網絡溫度補償模型, 能夠大大降低溫度對傳感器的影響, 同時提高整體溫度補償效率 。 |