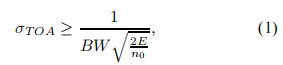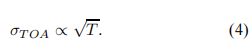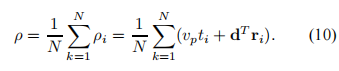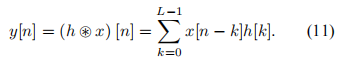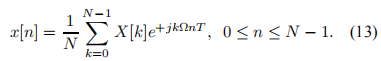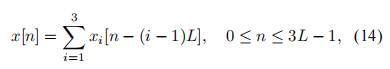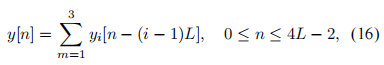這項工作介紹了USBL聲學定位系統在海上的設計、實現和驗證。從移動平臺發出的精心選擇的聲信號被水聽器陣列接收，并基于匹配的濾波器進行檢測。這樣就有可能確定到達時間(TOA)和估計發射極的位置。系統的性能依賴于對可能被加性噪聲和多徑現象破壞的期望信號的準確檢測和準確的TOA估計。將經典聲學純音脈沖與寬帶編碼擴頻信號(SS)進行了比較，提高了TOA分辨率，增強了多徑和噪聲抑制能力。

使用USBL近距離水聽器陣列接收SS信號需要先進的信號處理技術，只能使用數字信號處理器。因此，系統實現必須依靠實時數字信號處理技術，以提高性能和通用性。基于離散傅里葉變換(DFT)及其特性，研究了數字匹配濾波器的實現。該系統的總體性能是基于一系列海上測試的結果進行驗證的。

1.簡介

聲學定位系統的設計目的是跟蹤水下航行器或平臺的演變。這些系統依賴于測量運動目標發出的聲信號到達一組位置已知的接收器的時間。從TOA測量可以得到方位和/或距離，從而得到目標的位置。水聲定位系統通常用于各種水下應用，包括石油和天然氣勘探、海洋科學、打撈作業、海洋考古、執法和軍事活動。聲波定位系統可以達到幾厘米到幾十米的精度，可以在幾十米到幾十公里的操作距離內使用。性能在很大程度上取決于定位系統的類型和型號、針對特定應用的配置以及工作現場水聲環境的特征

1.1定位系統體系結構

水聲定位系統的經典方法將在本節中介紹，如[17]所示。聲學基線之間的距離(即有源傳感元件之間的距離)通常用來定義聲學定位系統。因此有三種主要類型:短基線(SBL)、超短基線(USBL)和長基線(LBL)。

1.1.1短基線

在一種SBL系統中，至少三個接收器，大約相隔20至50米，安裝在一艘水面艦艇的船體上。從聲信號的檢測和不同接收器的相對TOA測量，計算出一個方位。如果使用了飛行時間詢問技術(換能器應答器)，則還可以從SBL系統獲得到發射極的距離，從而可以得出位置。SBL系統提供的任何距離和方位都與安裝在船上的接收器有關，因此，SBL系統需要額外的工具，如垂直參考單元(VRU)、陀螺儀和水面導航系統(GPS)，以便在地球參考系統上提供位置。

1.1.2超短基線

類似于SBL，但這里的接收器間距很近(間隔小于50cm)。USBL接收器的近間距要求TOA估計的精度更高。通過這種方式，USBL系統依賴于接收器之間聲信號的相位差或相位比較，而不是相對到達時間的測量。

像在SBL系統中一樣，飛行時間詢問技術可以用來實現到發射器的距離。此外，USBL系統導出的位置是相對于安裝在船上的接收器而言的，因此需要VRU、陀螺儀和GPS提供地球參考位置。

短基線(SBL)和超排序基線(USBL)定位系統的主要優點是:

基于船舶的系統(不需要在海底部署應答器)。
較低的系統復雜度使得SBL和USBL相對容易使用。
良好的射程精度與飛行時間系統。這些系統的主要缺點是:
需要對系統進行詳細校準。
絕對定位精度取決于附加的傳感器(VRU和陀螺儀)。
在SBL系統的情況下，大基線(>40m)需要在深水精度。

1.1.3Long基線

部署了一個海底應答器網絡，其基線長達十公里。然后必須精確測量基線應答器的相對位置或全局坐標位置。至少需要三個應答器，但為了引入冗余可能會使用更多。通過測量應答器和被跟蹤車輛之間的移動時間，使用三角測量技術計算位置。每個應答器以不同的頻率應答，從而使它們的信號彼此區分開來。從LBL系統得到的位置是相對或絕對海底坐標，不像SBL和USBL，不需要額外的組件。

長基線系統的主要優點是:

非常好的位置精度獨立于水深。
大面積相對精度高。而這種系統的主要缺點是:
系統復雜度高
需要在每次部署時進行全面校準。
部署/恢復所消耗的操作時間。

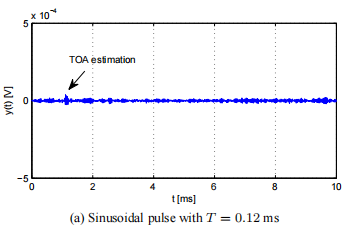
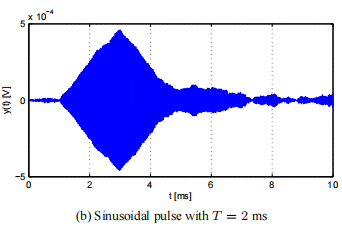
2、信號處理與定位

在本節中，對水下定位系統可能使用的兩種聲音信號進行了比較:傳統的正弦聲脈沖信號;和擴頻信號。研究了信號檢測和到達時間估計問題，提出了一種基于匹配濾波器的解決方案。給出了一種在參考坐標系中估計應答器位置的封閉方法。利用聲波的平面近似求出應答器的距離和方向。

2.1信號檢測與TOA估計

定位系統接收器有兩個主要功能。首先，它必須檢測水中是否存在預期的信號;如果是這樣，它必須估計信號的TOA。發射器的方向和距離是通過對不同水聽器的TOA測量來計算的，因此系統需要對可能被附加噪聲破壞的已知信號進行準確的檢測和TOA估計。

從信噪比(SNR)的角度來看，可以通過設計匹配濾波器來獲得檢測問題的最優解，該濾波器由一個線性系統組成，其脈沖響應是預期信號的時間反轉副本。濾波響應是采集信號與期望信號之間的相關性。到達時間對應于匹配濾波器輸出的峰值。

對于TOA問題，我們可以量化估計的不確定性。TOA估計值的標準差由[2]給出:

其中BW是信號帶寬的度量，為匹配濾波輸出時的信噪比，其中n0為輸入噪聲級，E為信號能量。從式1中我們可以看出，有兩種方法可以減少TOA估計方差，從而提高系統的可重復性:增加信噪比;或者增加信號的帶寬。

用于水下定位的經典信號是窄帶音突發，主要是因為傳輸和接收信號所需的電路簡單。讓我們看看如何減少這個特定信號的TOA估計方差。為了增加信噪比，我們必須增加所接收脈沖e的能量。對于正弦信號，能量與振幅和長度成正比。信號幅值受發射機功率的限制，因此通過發送更長的ping信號來實現更好的信噪比。

對于同一類型的信號，帶寬由其中T為脈沖長度，因此，為了減小TOA估計方差，信號持續時間必須減小。由(1)和(3)，且為E∝T，可得TOA估計為式(4)表示矛盾。當不可能進一步增加發射機功率時，必須延長信號以增加信噪比。這為檢測提供了更大的能量，但也會增加TOA估計的方差，這是不可取的。另一方面，為了達到最高的時間分辨率與音波爆發，最佳信號盡可能短。然而，這導致最佳信號的能量太少，無法在遠距離進行可靠的檢測。圖2顯示了兩個長度不同的正弦脈沖的匹配fifilter輸出。兩個信號都被相同的加性噪聲序列破壞。圖2a所示的較短脈沖在濾波器輸出中獲得了一個尖峰，但噪聲抑制能力較差。圖2b顯示，當我們延長脈沖時，噪聲抑制改善，但峰值的銳度下降。上面的討論代表了在加性白噪聲存在的情況下只有一個聲學信號的理想情況。然而，在水聲中通常有許多多徑信號，這些多徑信號是由反射引起的較晚時間到達的、振幅不同的信號的復制品。這種情景往往出現在淺層。

圖2:匹配的fifilter輸出

信號從海面(或海床)反射過來的水通道。圖3顯示了在2ms延遲和75%振幅多徑情況下，匹配濾波器對正弦脈沖的響應。

圖3:fifilter輸出與多路徑匹配

使用沒有窄自相關峰值的正弦脈沖，延遲信號的響應不能很好地與直接路徑分離。

我們在這里介紹了使用正弦脈沖的兩個主要缺點。

不可能同時增加范圍(信噪比)和精度(減少TOA估計方差)。
弱多徑拒絕。

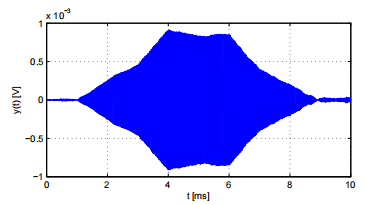
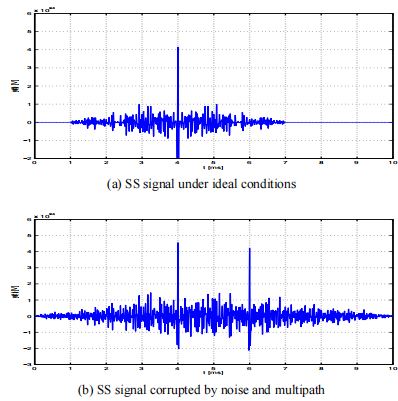
我們可以通過使用編碼擴頻信號來克服這些缺點。SS信號是自相關函數接近脈沖的寬帶信號。此外，對于SS信號，可以在脈沖長度增加[2]時保持帶寬。這樣，從(1)可以看出，可以通過延長SS脈沖，增加信噪比和系統范圍來增加信號能量，同時減小TOA估計方差，提高系統精度。圖4顯示了SS脈沖在理想條件下的行為，并受到噪聲和多徑的破壞。

圖4:匹配的fifilter輸出

圖4表明，使用SS信號，可以獲得匹配的濾波響應，其噪聲抑制特性類似于長正弦脈沖，但其銳度類似于短正弦脈沖。同樣，在多徑存在的情況下，對反射的響應和對直接路徑的響應被很好地分離，使探測器能夠可靠地找到第一個峰值。雖然SS信號是相對復雜的，低成本，高速，數字信號處理器(DSP)的可用性現在可以考慮在現實世界的應用中使用這些波形。從現在開始，在系統開發和測試期間，我們將使用SS聲信號。

2.2定位

輻射源的方向和距離是基于聲波的平面近似來計算的。這個問題如圖所示。兩個接收器(i和k)投影在XY平面上，傳播平面波，到達接收器的時間(ti和tk)和發射器的單位方向向量d = [d_x d_y d_z] ^T，意義相反，與傳播向量方向相同。平面波在接收器i和k之間傳播的距離由image.png給出其中v_p為水中聲速，r_i = [x_i y_i z_i] ^T, r_k = [x_k y_k z_k] ^T表示接收器在體幀上的位置。不使用矢量表示法eq. 5變成v_p(t_i - t_k) = - (d_x(x_i - x_k)+d_y(y_i - y_k)+d_z(z_i - z_k))。(6）

圖5:平面波近似

如果有N個接收器，就會有M個方程式，像eq. 6， {i = 1，…N;K = 1，…N; i6 = k}，等于M = n2 C N個接收器的所有可能組合。接收器之間的TDOA，∆=[∆1∆2…∆m]^t，∆1 = t1−t2，∆2 = t2−t3，…∆M = tN−1−tN，可由∆= Ctm生成，其中C∈RM×N為組合矩陣，t_m = [t₁…t_N] ^T是來自所有接收器的時間測量向量。同樣地，如果我們為接收器位置定義組合x = [x₁−x₂ x₂−x₃…x_N−1−x_N] ^T, y = [y₁−y₂ y₂−y₃ . .y_N−1−y_N] ^T, z = [z₁−z₂ z₂−z₃ . .z_N−1−z_N]^T，對于N個接收器，問題的概化可寫成vp∆=−(d_xx + d_yy + d_zz)。(7)[3]中給出的發射極方向的最小二乘解由d =−vpS #Ctm給出，(8)

其中S = [x y z] e S # = (S T S)−1S T。同樣利用平面have近似，發射極到接收器i的范圍由ρei = vpti給出，i = 1，…N，到體幀原點的范圍由ρi = ρei + dT ri，(9)其中d是先前計算的發射極方向向量。

將所有N個接收器的估計值取10的平均值

3、系統開發

研制的USBL聲定位系統可分為發射和接收兩部分。建造發射箱并不是這項工作的目的，我們使用了一個現有的盒子，它能夠生成預記錄在內存中的DSSS聲信號。另一方面，接收機的開發和編程是主要任務。接收盒的核心是DSP，可以提高USBL聲學定位系統的性能和通用性。使用德州儀器公司的TMS320C6713浮點DSP，工作頻率為225MHz。在執行任何DSP算法之前，信號必須是數字形式的。這個任務是由一個16位，250 KSPS, 4通道a /D轉換器完成的。系統受控(啟動/停止、操作模式、數據傳輸……)通信由SMSC LAN91C111以太網板保證。接收箱電子設備安裝在一個矩形的角度防濺外殼內，配有四個水聽器輸入連接器，一個用于PPS信號訪問的GPS天線，一個外部電源和一個以太網端口。發射箱如圖所示6.

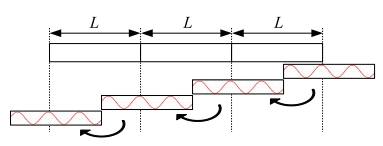
圖6:接待室

3.1收購

這個過程從4個水聽器陣列開始，基于壓電換能器將聲波轉換為電信號。電信號被4個可變增益放大器放大。這些精密的模擬信號必須轉換成數字形式。該過程由ADC轉換器執行，包括以下步驟:首先對信號進行采樣，將模擬信號轉換為離散時間連續幅值信號;每個信號樣本的振幅被量化為2個16級中的一個;離散的振幅電平被編碼成不同的16位長度的二進制字。這個二進制字，表示水聽器“偵聽”的聲波的數字形式，必須臨時存儲在DSP內部存儲器中，以便進行處理，以檢測預期信號的存在，并計算發射器的方向。

為了解決數字數據存儲問題，實現了FIFO(先進先出)數據緩沖區。緩沖區被劃分為塊，當ADC獲取新數據時，緩沖區中的數據正在被處理。當采集完成后，最老的數據塊被最新的數據所取代，新的循環開始。方塊的數量和長度是現在的主要問題。這是一個微妙的問題，因為在一個塊采集的時間內，由L/fs給出，其中L是塊長度，fs是采樣頻率，DSP必須能夠處理緩沖區中所有塊中的數據。以這種方式，塊必須足夠大，以便給數據緩沖區處理時間，但又不能太大，因為內存限制。這種權衡導致我們使用與預期信號相同長度的塊L。

緩沖區硬件實現的示意圖如圖7所示，以及預期信號通過緩沖區的過程。由于系統有四個水聽器，將有四個先進先出緩沖器用于數據存儲，如圖所示7.

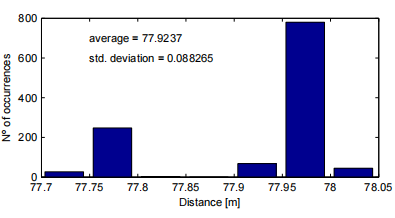
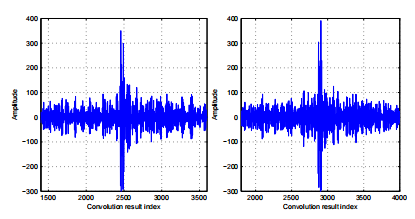
圖7:長度為3L的FIFO數據緩沖區

當系統指示所期望的信號存在時，它可能完全或只是部分在緩沖區中。因此，為了得到準確的結果，在估計信號到不同水聽器的TOA和計算發射極位置之前，必須確保預期信號完全在緩沖器內。使用三個長度為L的塊的選擇是因為我們希望這種情況至少發生兩次，而3是確保這種情況發生的最小塊數量。像這樣，fifirst檢測總是被忽略，當保證信號完全在緩沖區內時，只接受第二個連續檢測。此時，采集暫時停止，以便進行TOA估計和發射極位置計算。

需要注意的是，如果只使用兩個L長度的塊，則無法保證這一點。

3.2處理

在第2.1節中，我們說過使用匹配濾波器是信號檢測的最佳解決方案。因此，將在DSP中實現一個數字匹配濾波器。輸出到緩沖區中的一組數據x[n]的數字濾波由x[n]與濾波脈沖響應h[n]之間的數字卷積(卷積和)給出。

因為匹配濾波的目的是執行期望信號與采集數據的cor -關系，它的脈沖響應h[n]將是在ADC工作頻率fs處采樣的期望信號的副本。然而，卷積是一項計算量很大的工作。標準卷積算法具有二次元的計算復雜度，即使使用快速數字信號處理器，其實時計算機實現在大多數應用中也是不可能的。在這種情況下，引入離散傅里葉變換(DFT)的概念變得非常重要，因為使用DFT特性可以加快相關計算的速度。令{x[n]} = {x[0]， x[1]，…， x[N−1]}為采樣序列，其中N為樣本個數。它的Dis - crete傅里葉變換是復值序列{X[k]} = {X[0]， X[1]，…， X[N−1]}在頻域，具有相同的長度N，由其中Ω = 2π/NT, T為采樣周期。離散傅里葉反變換(IDFT)在給定其DFT {x[k]}的情況下恢復序列{x[n]}，它被定義為

圖8顯示了用于相關目的的有用的DFT性質。用一種非常簡單的方式，我們可以說可以將時域卷積h[n]⊛x[n] '改變為頻域乘法h[k] x[k]。該方法需要計算一次DFT (H[k]永久存儲在DSP內部內存中)、一次乘法和一次IDFT，將計算復雜度從o(N2)降低到o(Nlog2N)。當需要卷積的樣本數量足夠大時，就像我們的例子一樣，這種性能改進，以及快速DFT算法(FFT)的使用，是非常重要的，因為它使實時卷積實現成為可能。即使使用上述解決方案，卷積實現也可以進一步改進。如3.1節所述，數據緩沖區由三個內存塊組成，大小與預期信號的L相同，在每個采集周期結束時，只有其中一個塊被更新，即其他兩個塊被移動。這樣，當只有三分之一的數據與之前的采集周期不同時，執行3L大小的卷積就沒有意義了。讓我們考慮數據緩沖區3L長度序列{x[n]}作為三個L長度序列{x1[n]}， {x[n]2}和{x[n]3}的和，如下所示:每個序列{xi [n]}表示數據緩沖區的第i個塊。將(14)替換為由(11)給出的匹配fifilter輸出其中yi [n] = (h⊛xi) [n]是fifilter對第i塊數據的響應。正如我們從(16)中看到的，可以將期望信號與整個數據緩沖區的卷積計算為與每個單獨塊的卷積之和。因此，在每個采集周期中，我們可以執行L大小的卷積而不是3L大小的卷積，可以顯著提高時間性能。這種卷積方法被稱為重疊-相加，因為每個h⊛xi的卷積長度為2L−1，當h⊛x1與h⊛x2相加，h⊛x2與h⊛x3相加時，L−1元素會重疊。

3.3決定

在執行匹配濾波卷積后，系統必須決定預期信號是否存在于數據緩沖區中。為了研究決策準則，我們應該回頭看圖4a和圖4b，其中濾波器對DSSS信號的響應是給出的。決策準則背后的思想是將匹配fifilter輸出的最大值與其平均絕對值進行比較。由于噪聲的存在，這是采集到的數據中未知的組成部分，總是會有某種程度的不確定性。然而，由于有一個大大高于平均絕對值的最大值是一個與濾波器對預期DSSS信號的響應相關的特征，而不是對噪聲的響應，我們將認為這兩個值之間的差異最大，預期信號出現在緩沖區的機會也就越大。通過這種方法，我們為系統定義了一個閾值，并認為期望信號出現時當預期信號出現時，系統必須等待下一個采集周期，只有連續的第二次檢測才能保證信號完全在緩沖區中，如3.1節所述。

3.4位置計算

與所有四個水聽器都在持續進行的采集不同，只對四個水聽器中的一個實現了采集數據的處理和信號存在性決策。我們記得，整個處理和決策必須在少于一個緩沖區塊獲取的時間內執行，這是實現的最關鍵點。因此，不可能處理所有四個緩沖區中的數據。盡管如此，當選擇用于實時處理的數據緩沖區中檢測到預期信號時，采集會暫時中斷，并處理剩下的三個數據緩沖區，以查找信號TOA。根據2.2節中介紹的研究計算位置，在什么采集重新啟動后。

4海上試驗

一旦實施完成，就進行了一系列海上試驗。測試于2009年6月22日至26日在奧爾塔城進行。由于位置結果是在USBL陣列的坐標坐標系中表示的，因此最好陣列相對于地球坐標坐標系保持靜止，否則即使在發射極位置靜止的情況下，USBL陣列的運動也會影響位置計算。因此，試驗是在港口內進行的。這樣就可以牢牢地固定陣列，確保定位結果不受其運動的影響。然而，港口內的多徑和噪聲存在性要強得多，因此影響了測試結果。試驗分為兩類:靜態和動態。由于計算方法不同，這兩種方法的結果分別對距離和方向估計進行了分析，如2.2節所示。

4.1平穩性試驗

在靜止測試中，發射器被綁在一個橋墩上，橋墩上的波動可以忽略不計，系統運行20分鐘。通過DSP處理得到的試驗平穩距離結果直方圖如圖9所示。從圖9中我們可以看到，距離結果主要劃分在兩個非連續子區間之間，[77.70;77.80]m和[77.90;78.05 m。發射器和USBL陣列都是靜止的，這是一個意想不到的結果。為了了解它發生的原因，我們應該觀察用來決定信號是否存在和計算發射極距離的數據。兩種不同檢測的匹配濾波卷積如圖10所示。

圖9:車站測試距離結果直方圖

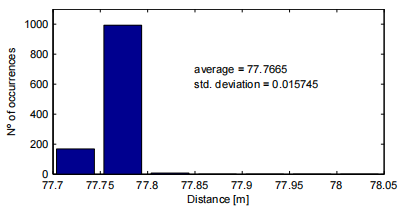
圖10:匹配的濾波器卷積

從圖10a和10b可以看出，匹配濾波卷積有兩個非常接近的最大值。因為信號TOA是用卷積的峰值來計算的，當絕對最大值是第一個距離將位于最近的子區間，當絕對最大值是第二個距離將位于最遠的子區間。在詳細分析了所有檢測的四個通道的卷積結果后，我們可以說，圖10a和10b代表了測試期間發生的情況。在圖11中，給出了不同通道的兩個卷積最大值之間的時間差的直方圖。

如圖11所示，兩個卷積最大值之間的時間差因信道而異。通道4卷積的差異更大，通道3和通道1和2的中間差異更小。綜合以上說明，已知通道4連接最深的水聽器，通道3連接最靠近水面的水聽器，通道1和通道2連接中間深度的水聽器，我們發現匹配濾波器卷積中的第二個最大值是由海面上的信號反射引起的，是由直接路徑信號到達引起的第一個最大值。

為了解決這一多路徑檢測問題，我們必須修改TOA估計方法。當(17)給出的決策因子為真時，我們不將TOA估計為絕對最大值位置，而將TOA考慮為超過決策閾值的第一個最大值的位置。在圖12中，我們再現了之前圖9中給出的結果，這些結果是用新的TOA估計方法對測試期間獲得的數據進行后處理后得到的。

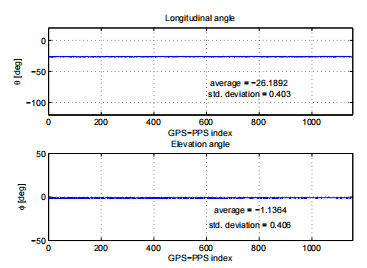
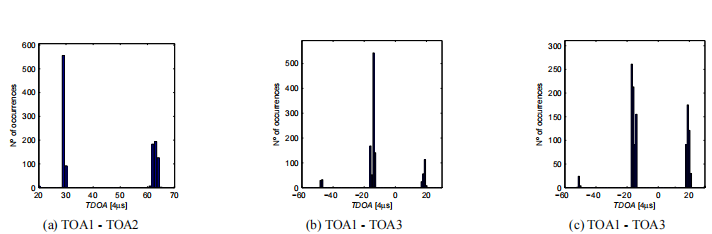
圖12采用新的TOA估計方法的車站試驗距離結果直方圖

從圖12可以看出，采用新的TOA估計方法，距離結果不再劃分在兩個不連續子區間之間，距離標準差由8.8降低到1.6cm。通過這種方式，系統對多路徑的拒絕大大提高了，從而提高了系統的全局性能。如果說多徑效應在計算輻射源距離時造成了厘米量級的誤差，那么在計算輻射源方向時，這些誤差則是幾十度量級的。通過DSP處理得到的試驗平穩方向結果如圖13所示。從圖13可以看出，方向計算得到的結果非常不一致。

然而，為了理解這種糟糕性能的原因，最好看看用于計算發射器方向的數據，而不是最終的結果。如2.2節所述，方向從信號TDOA到不同的水聽器計算。在圖14中，我們給出了4個水聽器之間TDOA的3個直方圖。

我們看到圖13中不一致的方向結果被圖14a, 14b和14c中不一致的TDOA估計所證明。與之前的距離計算(圖9)一樣，TDOA結果被劃分在非連續子區間之間。同樣，30到40個樣本的子區間之間的時間差是相似的(見圖11)，這表明問題可能是由信號反射引起的。因此，我們將嘗試用同樣的方法來解決這個問題:修改TOA估計方法，避免多徑檢測。在圖15中，我們再現了圖14所示的結果，這些結果是用新的TOA估計方法對測試期間獲得的數據進行后處理后得到的。

正如預期的那樣，新的TOA估計方法大大改進了TDOA估計，現在的TDOA估計精度約為8μs(2個樣本)。用TDOA數據計算的發射體方向如圖16所示。將其與測試期間獲得的方向(圖13)進行比較，可以明顯看出系統性能大大增強，兩個角度估計的標準偏差約為0.4度。

圖16:采用新的TOA估計方法的臺站測試方向結果

當涉及到時間延遲估計時，有一個非常常見的方法:數據之間的相互關聯。為了尋找不同水聽器的信號TDOA，在后處理分析中還采用了互相關的方法。這里沒有給出得到的結果，但它們揭示了一個有趣的特征:互相關性能取決于被處理的通道。TOA1- TOA2估計的性能相似(通道1和2連接到相同深度的水聽器)，其他兩個通道的性能較差。信號反射和水聽器放置在不同深度也證實了這一結果。

圖14平穩試驗方向結果TDOA直方圖

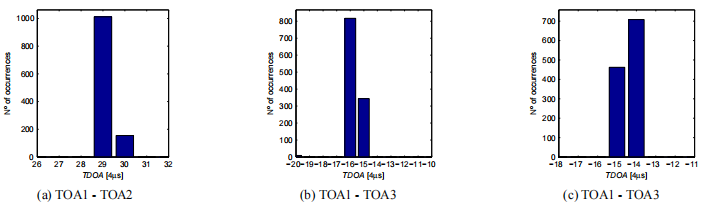
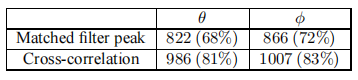
圖15采用新的TOA估計方法的平穩試驗方向結果TDOA直方圖

4.2動態試驗

為了進行動態測試，發射極被安裝在用GPS記錄位置的船上。可以測試的距離和角度間隔非常有限。盡管如此，在港口內進行了動態測試，以允許USBL接收陣列的充分緊固，如本節開始所解釋的。動態測試持續時間為1445秒(約24分鐘)。由于發射頻率是每秒一個信號，1445將是探測到的最大數量。然而，有203個(占總量的14%)的排放被損失了。圖17顯示了動態試驗的距離結果。排放損失在0米距離處繪制。除了損失的發射外，還有一些探測會導致明顯錯誤的距離結果。這些錯誤的結果是由直接路徑信號丟失和相應的多路徑檢測造成的。為了量化這些情況，我們考慮最大速度為4m。S−1對于船和特定距離的結果，如果它意味著比上次檢測的速度更高，則被分類為不正確。這樣，從1242次檢測中，有1210次被分類為正確的(1445次總排放的84%)。在檢測的百分比和結果分類為正確的情況下，動態距離計算性能是令人滿意的。

在評估系統性能時，計算輻射源的方向也采用相同的策略。方向結果未繪制，但正確結果的百分比見表1。我們比較了兩種不同的TDOA估計方法得到的方向結果:第一卷積最大值超過決策閾值和數據互相關。現在只使用導致正確距離結果的1210個接收。

表1:動態測試方向結果

這兩種方法都會導致相似的性能，但與平穩檢驗不同的是，交叉相關現在呈現出略好的結果。此外，縱向和仰角之間的性能非常相似。這一事實可以被質疑，因為正如我們之前所說，交叉相關方法的性能取決于所處理的通道，而TOA1- TOA2估計的性能要好得多，通道與水聽器連接在相同的深度，因此足以計算縱向角。然而，在2.2節中，我們開發了一個發射器方向的最小二乘解，使用所有4個通道來計算任何角度。這樣，可以增加冗余，但放置在不同深度的水聽器的低性能估計TDOA可能會破壞縱向角度計算。為了確認我們重復方向計算，現在不進行最小二乘最小化，使用通道1和2(相同深度)計算縱向角，使用通道3和4(不同深度)計算仰角。

表2:無最小二乘最小化的動態測試方向結果

從表2中，我們再次看到相互關系呈現出稍微更好的結果，但縱向和仰角之間的表現現在有很大的不同。縱向角性能明顯提高，接近100%的正確結果，仰角性能保持在相同的精度水平。這些結果表明，最小二乘最小化會破壞系統的性能。將通道1和2與通道3和4分離，我們失去了冗余，但通道3和4的較不準確的TDOA估計不會破壞縱向角度計算。盡管如此，當TDOA估計誤差在通道之間相似時，最小二乘最小化應該是一個很好的選擇。

5、結論

本工作介紹了USBL聲學定位系統的設計、實現和海上驗證。信號檢測和TOA估計基于匹配的濾波響應，這導致了最高的信噪比。將經典聲學純音脈沖與寬帶編碼擴頻信號進行了比較，得到了更高的TOA分辨率和更強的多徑和噪聲抑制能力。發射器的位置是計算訴諸于聲波的平面近似。最關鍵的開發任務是數字濾波器的實現。數字濾波由信號卷積組成，必須在實際時間內完成。由于使用了DSP和處理技術，使得實時實現成為可能，這些技術大大減少了卷積時間(基于DFT特性)。為了給出系統電位的全局概念，我們在圖18中比較了發射器的GPS跟蹤與USBL定位計算的正確距離結果和沒有最小二乘最小化得到的縱角。

參考文獻：

[1] A. Alcocer, P. Oliveira, and A. Pascoal. UnderwaterAcoustic Positioning System Based On Buoys With GPS. Proceedings of the Eighth European Conference on Underwater Acoustics, 8th ECUA, June 2006.
[2] Thomas C. Austin. The Application of Spread Spectrum Signaling Techniques to Underwater Acoustic Navigation. Proceedings of the 1994 Symposium on Autonomous Underwater Vehicle Technology, 1994.
[3] P. Batista. Controlo de Ve′ıculos Aut′onomos Baseado na Informac¸˜ao Directa de Sensores Ac′usticos. Relat′orio de trabalho final de curso, Universidade T′ecnica de Lisboa - Instituto Superior T′ecnico, Setembro 2005.
[4] R. Cusani. Performance of Fast Time Delay Estimators. IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37(5):757–759, May 1989.
[5] F. Gustafsson and F. Gunnarsson. Positioning Using Time-Difference Of Arrival Measurements. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003.
[6] Emmanuel C. Ifeachor and Barrie W. Jervis. Digital Signal Processing. A Practical Approach. AddisonWesley Ltd., 7th edition, 1998.
[7] Sonardyne Inc. http://www.sonardyne.com/, 2009.
[8] F. Lima and C. M. Furukawa. Development and Testing of an Acoustic Positioning System - Description and Signal Processing. Proceedings of the IEEE 2002 Ultrasonics Symposium, 2002.
[9] Isabel M. G. Lourtie. Sinais e Sistemas. Escolar Editora, 2nd edition, 2007.
[10] P. H. Milne. Underwater Acoustic Positioning Systems. Gulf Publishing Company, 1983.
[11] Sanjit K. Mitra. Digital Signal Processing. A Computer-Based Approach. McGraw-Hill, 2nd edition, 2001.
[12] M. Morgado, P. Oliveira, C. Silvestre, and J. F. Vasconcelos. USBL/INS Tightly-Coupled Integration Technique for Underwater Vehicles. Proceedings
Of The 9th International Conference on Information Fusion, 2006.
[13] Marco M. Morgado. Sistema de Navegac¸˜ao Inercial com Ajuda USBL. Relat′orio de trabalho final de curso, Universidade T′ecnica de Lisboa - Instituto Superior T′ecnico, Setembro 2005.
[14] J. O. Smith and J. S. Abel. The Spherical Interpolation Method of Source Localization. IEEE Journal of Oceanic Engineering, vol. 12(1):246–252, 1987.
[15] D. Thomson and S. Elson. New Generation Acoustic Positioning Systems. Oceans 2002, vol. 3:1312–1318, Oct. 2002.
[16] Robert J. Urick. Principles of Underwater Sound. Peninsula Publishing, 3rd edition, 1983.
[17] K. Vickery. Acoustic Positioning Systems. A Pratical Overview Of Current Systems. Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles, August 1998.
[18] K. Vickery. Acoustic Positioning Systems. New Concepts - The Future. Proceedings of the 1998 Workshop on Autonomous Underwater Vehicles, August 1998.
[19] J. Yli-Hietanem, K. Kalliojarvi, and J. Astola. LowComplexity Angle of Arrival Estimation of Wideband Signals Using Small Arrays. Proceedings Of The 8th IEEE Signal Processing Workshop on Statistical and Array Processing, 1996.