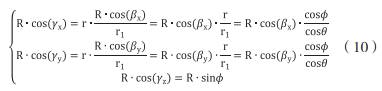|
超短基線水聲定位系統誤差校準方法綜述一、引言 超短基線水聲定位系統（USBL）以數據和圖形方式實時 顯示水下目標的定位，屬于水聲定位系統的一種，于20世紀70年代問世，優點有基陣尺寸小、安裝便捷，測量準確， 未來將有更為廣泛的應用。國外（USBL）技術發展相對成 熟，一些公司已推出較為成熟的產品，因此我們可以通過國 外已研制成功的相關產品來實時了解國際上在水聲定位技術 方面的研究進展。與此同時，由于國外技術封鎖以及一些歷 史原因，國內對于（USBL）的發展較晚，但仍有相關單位正 在積極研究國產的超短基線定位系統。本文對國內外目前有 關超短基線校準方法的進展進行了總結。 二、USBL 組成及定位原理 超短基線水聲定位系統集成了水面船用設備和應答器 （見圖 1）。前者的基本構成單元有信號處理單元、聲學換能 器陣和外圍輔助傳感器三部分。在應用中，聲學換能器陣往往是固定到船只的底部或側舷。應答器則需要設置在水下移動載體上，如果采取同步時鐘觸發工作模式，還需連接同步時鐘，向水體中發射與接收相應信號，傳輸相互通信的數據，其指向性輻射聲波的范圍是半球形，無論是何種深度水下和傾斜角度，都不會妨礙超短基線水聲定位系統的正常運行。
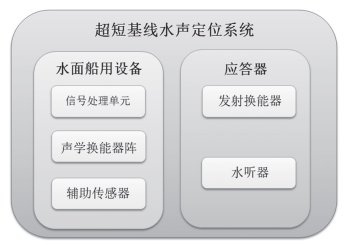
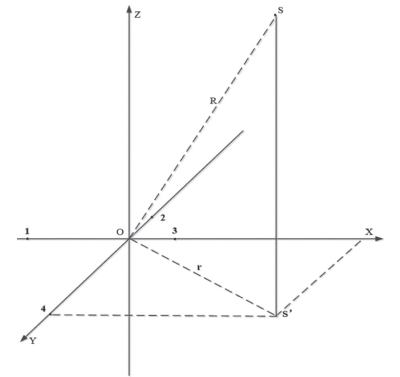
圖 1 超短基線水聲定位系統基本組成 水下目標物方位的確定，是利用測量信號的到達方位和距離來實現的。測量信號到達接收基陣基元之間的相位差用于完成測向的任務。設超短基線基陣的四個基陣單元，形成了基陣一個左手坐標系，其中原點坐標是基陣中心 O，分布在 x 軸上的有 1 號和 3 號陣元，排列在 y 軸上的是 2 號和 4號陣元，陣元之間的距離為 D（指 1、3 陣元間距和 2、4 陣元間距），如圖 2 所示：
圖 2 超短基線水聲定位系統定位原理圖 圖 2 中需要確定的目標物位置是 S，目標徑矢為 O—S，α=[αx αy αz]' 為方向角向量表示，目標斜距為 R，假設基陣尺寸相對于目標斜距很小，使用平面波近似方法，得出如下式：
其中 c 為水中聲速， τ13、 τ24 分別為 1、3 陣元和 2、4 陣元由于不同的速度，傳輸距離，以及不同的時間，各信號出現了不同的時延現象，也就是接收信號時延差，從先驗信息來決定 cos（ αz）的符號。
其中： 在斜距 R 已知時，可得到以基陣中心為原點的大地坐標 三、聲線修正的原理 在聲速剖面上根據目標深度進行等深度分層，每層近似為由恒定聲速構成，也就是將聲速的連續變化分布形態分解為每層為同一種聲速層的聲速分布，并用折線逼近形式表示實際聲線軌跡，聲速傳播軌跡示意圖如圖 3 所示。
圖 3 聲速傳播軌跡示意圖 將水面到水下目標的垂直深度分為 N 層，且每層等深，以恒定聲速傳播，聲速軌跡為折線，則用聲線軌跡圖求每一層的水平距離 ∆xi 和 ∆ti， ∆Zi 為每層深度值，其中 Z0=Z1……Zi， i=（0,1,2,…,N）。
在分層介質中，射線聲學遵循 Snell 定率。
式中： C0 和 θ0 為初始聲速和初始掠射角， Ci 為第 i 層處的聲速， θi 為第 i 層邊界處的掠射角。總的聲線行程 L 和聲線單程時間 t 等于 N 層的 ∆L 和 ∆t 的疊加，于是
另外，水聲信號從水下目標 S 處出發，以類似球面波的形式傳播到換能器接收基陣 O 處所需要的總時間 t，測算方式可以是應答模式或是同步模式，基于系統對于水下目標深度的可測性，對水下目標 S 進行分層，直到最末端一層上，利用公式（5）、（7）反推 θ0，基于 C（i i=0,1,2,…,N）的已知數值，要求值 θ（i i=0,1,2,…,N），則通過公式（5）用 θ0 與 Ci （ i=0,1,2,…,N），隨后，代入公式（7），綜合整個解算方程看來，僅僅存在一個未知項 θ0，因為整個公式需要復雜的計算步驟，很難直接計算出 θ0，于是，工程實際應用中，通常采用編程方式，通過“夾逼法”的應用得出初始掠射角 θ0。 三、聲線彎曲的修正方法 由于非均勻介質，容易引起的聲線彎曲變形，從而影響了 USBL 系統精確定位，于是，就需要修正聲線。不同于長基線定位系統，超短基線的聲線彎曲誤差修正方法需要同時修正距離和角度這兩個方面。 （一）距離修正方法 計算而得入射聲線與以基陣中心為原點的大地坐標系的方向角余弦向量 cos（
其中 θ 為入射聲線到達基陣中心為原點的大地坐標系下的水平面的掠射角。在不發生反轉的情況下，在已知聲速分層分布、發射點的深度和接收點的深度條件下，由射線聲學理論，可反推出始于聲源的聲線軌跡，以及收發信號間的直線斜距 R，來修正定位距離。當發現掠射角 θ 有誤差時，只要在小范圍搜索 θ 的周邊，即可確定收發之間的水平距離。 （二）方向角修正方法 設收發之間的連線與以基陣中心為原點的大地坐標系的方向角向量為 =[δx δy δz]'，則可知目標在以基陣中心為原點的大地坐標系的坐標為：
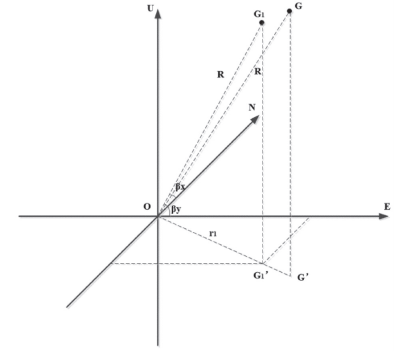
設定以基陣中心為原點的大地坐標系為 O-NEU 坐標系，其中 O 為基陣中心。設定 G 為未修正向角的目標位置G1，其在水平面上的投影為 G1'， G1' 與基陣中心之間的水平距離為 r1，則 與水平面 NOE 的夾角為 θ。設定目標真實位置為 G，其在水平面 NOE 上的投影為 G'， G 與基陣中心點之間的水平距離為 r， 與水平面 NOE 的夾角為 ，且
圖 4 方向角修正原理圖 因此根據幾何關系可得到：
以上即為聲線彎曲修正后的 USBL 定位解算公式。 四、USBL 誤差校準技術研究現狀 （一）USBL 安裝誤差校準技術國外研究現狀 從 1997 年 至 2010 年 前 后， 海 底 測 地 已 經 可 以 利 用GPS 技 術 和 有 效 聲 速 理 論 來 實 現 海 底 目 標 厘 米 級 定 位。Opderbecke 提出水面船沿任意航跡行駛，并多方向采集數據，此時以水下固定目標為參考。2002 年，Faugstadmo 等人提出利用具有圓形等一系列形狀的測量船運行軌跡對角度偏差進行校準。為了提高校準精度，Faugstadmo 等人在校準方案中加入了動力定位裝置。2003 年美國的 Philips 三篇 USBL 海上安裝校準的論文公開，但是并沒有包括校準的算法及公式，但沿用了法國海洋開發研究所的 Jan 提出的計算策略，具體是找出水下同一定位目標，標較其安裝位移偏差和安裝旋轉偏差。此外，來自斯坦福大學的 J.David Powell 等人在對基陣與船體偏差進行校準的過程中采納了空間角度測量。挪威的 Pettersen Hansen 等人通過鎖相等技術對時間以及相位進行檢測，得到相位值精度較高。2008 年，Chen 等人提出的圓形航跡校準以海底固定目標作為圓心，削弱了聲速對應答器水平定位的影響。區別于一般的校準算法：Chen 等人利用由于角度偏差導致的目標定位誤差與測量船運行軌跡之間的關系，根據已知的水下固定目標位置，在各種半徑的圓形軌跡下，根據 USBL 聲學定位的不同結果在聲學坐標系中所投影的不同形狀對角度偏差進行估計。 由于圓形航跡可能在實際工作中發生畸變，此時可能導致校準精度降低，2013 年，Chen 等人又提出了當海底目標固定不變，此時測量船采用直線軌跡的校準方法。 （二）USBL 安裝誤差校準技術國內研究現狀 與此同時，國家“863”等一系列研究規劃，十分重視研究 USBL 系統，2005 年唐秋華和吳永亭等人首次在國內明確提出 USBL 的校準算法。該思想類似但不同于 Jan 的方法，它是將安裝校準等效于參數估計問題，用最優化方法來估計安裝位移偏差和安裝旋轉偏差的分量，得出其基于最小二乘的各個量值。同年，哈爾濱工程大學的喻敏在研制長程超短基線時，采用該方法改進數值解法，提出了一種魯棒算法。主要適用于淺海條件中的校準，通過航船繞行獲取數據，并取得了較好的定位結果。論文沿用吳永亭提出的觀測方程并改良了校準算法，又進一步深入地研究了迭代最小二乘、穩健估計算法以及序貫最小二乘。 2006 年，海洋一所劉焱雄等人提出了一種非線性迭代算法來計算位置安裝偏差，該算法提供了解決思路，但在水下工作中會導致估計精度低、結果易發散等不可避免的情況。同年臺灣國立中山大學亞太研究中心的應用海洋學院物理和海底技術研究所，給出了另外一種校準算法。該算法根據旋轉角影響下的三維定位誤差，幾何圖解法求解，同時亦要求水下目標有可循的運動軌跡，但該算法不適用于國內系統。2007 年，哈爾濱工程大學的鄭翠娥在 USBL 的水下平臺探討USBL 安裝校準，引用了校準的觀測方程，并納入聲線彎曲的影響因素。他的研究采用兩步校準觀測方程，一是方程保持不動，二是觀測量設定為聲線與基陣的入射夾角。測線選取問題是她的首創，以圓航跡為例，說明安裝旋轉誤差影響下的定位。 2010 年，楊保國針對角度偏差校準，分析了角度偏差的觀測模型，對比了多種解算方法。2013 年，李昭等人分析了聲速誤差對校準的影響，提出了在校準航跡中將圓形與直線相結合的觀點。 五、結語 參考文獻： [4] 喻敏 . 長程超短基線定位系統研制 [D]. 哈爾濱：哈爾濱工程大學，2005. 班寧產品匯總 |
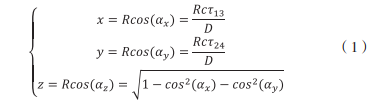
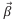為入射聲線與原點取基陣中心的大地坐標系的方向角向量，從坐標旋轉理論得出：
為從載體坐標系到大地坐標下的旋轉矩陣，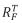
為從基陣坐標系到載體坐標系的旋轉矩陣。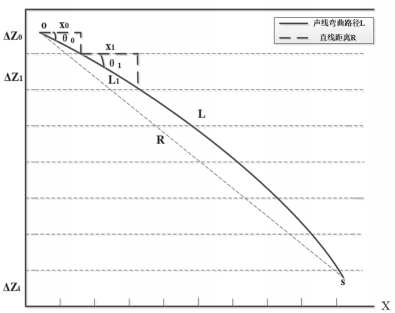
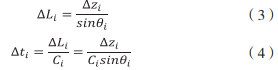
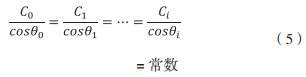
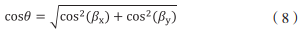
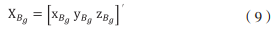
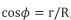。聲線投影在水平面上的位置，不會因為聲線彎曲而改變，所以， G1 和 G 在水平面上的投影呈同一直線，平面 OG1G1' 與平面 OGG' 重合。方位角修正原理圖如圖所示：
