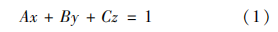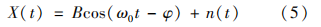隨著水上交通的發展單一的沉管定位方法已經很難滿足施工的需求隨著沉管的施工環境向遠岸、深水發展將多種定位方法進行組合，集合成綜合定位系統已成為現代沉管隧道沉放定位技術的主流。其中將水聲定位技術與廣域差分ＧＰＳ定位技術相結合可獲取沉管的大地坐標，且受環境因素影響較小，無需安裝測量塔，已成為解決深水沉管隧道管節沉放的有效途徑。

       提出將沉管沉放定位分為兩個階段:粗測階段及精測階段。在粗測階段將超短基線(ＵＳＢＬ) 聲學定位系統與 ＧＰＳ 組合，對下沉階段的管節位 姿進行實時測量，引導待沉管節沉放至預定位置，省去測量塔的安裝，提高施工深度，在精測階段，由精測定位系統(如超聲波定，機械定位) 完成沉管最終對接，本文重點圍繞粗測階段，詳細給出基于水聲定位系統和ＧＰＳ定位系統的沉管定位方案。

１ 沉管定位方案

１. １ 方案布置

       針對待沉管道下沉施工階段，提出基于超短基線定位系統對待沉管節姿態進行實時測控。安裝在施工平臺(如駁船)舷側的超短基線系統以聲波作為載體，對固定在待沉管節表面的應答器進行定位，駁船上安裝有 ＧＰＳ 天線以及姿態傳感器，用于將超短基線坐標系下的定位信息，轉換到大地坐標中，因此，需要建立３個坐標系: 以ＧＰＳ天線為原點的大地坐標系、以駁船重心為原點的船心坐標系和以超短基線基陣中心為原點的，基陣坐標系，通過姿態傳感器測量的船姿態信息及ＧＰＳ天線的大地坐標，根據歐拉旋轉矩陣對３個坐標系進行轉換，最終可獲取待沉沉管在大地坐標系中的位姿信息，見圖 １

圖 １ 基于ＵＳＢＬ定位系統的沉管定位方案

       從管節下沉開始，位于沉管上表面的應答器便不間斷地發射預置脈沖信號，基陣持續接收脈沖信號，超短基線系統根據基陣陣元間的相位差解算出應答器在基陣坐標系中的位置，并通過位姿解算方法獲得沉管的位姿信息，然后 通過坐標轉換獲取沉管在大地坐標系中的絕對位姿信息，最終，顯示器實時顯示沉管在大地坐標系中的三維位姿，對現場施工進行連續監控。

１. ２ 位姿解算

       已知應答器安裝在待沉管節上，且待沉管節上的應答器在一個平面上，即可根據三點共面條件，通過求解應答器坐標獲取待沉管節平面上的３個點，繼而求出待沉管節平面在基陣坐標系中的姿態信息。

設待沉管節平面的平面方程為

式中 Ａ、Ｂ、Ｃ 為未知參數，至少需要３個不共線的坐標，可解出Ａ、Ｂ、Ｃ之后可通過平面的法線式方程得到待沉管節平面在基陣坐標系中的法向矢量，即待沉管節平面的方向余弦向量。

設ＵＳＢＬ基陣所在的平面為 ＸＯＹ則基陣平面的法向量就可表示為

則從管節 平面法向量到 ＵＳＢＬ基陣平面法向量的旋轉矩陣可表示為

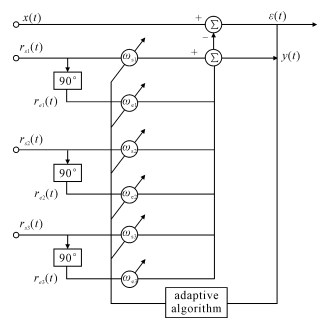
設從ＵＳＢＬ平面到待沉管節平面的繞基陣坐 標軸旋轉的歐拉角為 θｘ、θｙ、θｚ則 Ｒ 是關于 θｘ、 θｙ、θｚ 的旋轉矩陣，根據旋轉矩陣Ｒ即可以求出待沉管節平面的姿態角度 。

１. ３ 多址定位技術

       由位姿解算方法可知，對沉管定位過程中需要對多個應答器(≥３)進行定位，因此涉及水下多址定位技術，即每個應答器通過發射不同形式的脈沖信號，超短基線系統根據接收到的脈沖信號來分辨不同的應答器，并確定每個應答器在基陣坐標系下的坐標，由于自身具有調節參數的能力以及對信號和噪聲的先驗知識要求少，且在高信噪比下，Ｎｏｔｃｈ濾波器有著良好的相位差估計 能力，可以作為超短基線系統多址信號檢測器及相位差估計器。

       首先根據應答器的個數來設計可用帶寬，Ｎｏｔｃｈ的每路參考信號的頻率分別對應應答器的中心頻率，假設需要安裝３個應答器，則其對應的３路并聯Ｎｏｔｃｈ濾波器的結構圖見圖２。

對每一個應答器Ｘ(ｔ)為基陣接收的信號

式中:ｎ(ｔ)為背景噪聲

圖２ ３路并聯的Ｎｏｔｃｈ濾波器

ｒｉ(ｔ)為兩路正交的參考信號，ｙ( ｔ)為參考信 號正交信號的內積，ε(ｔ)為接收信號與參考信號內積的誤差。對參考信號的頻率已知，分別對應單個應答器發射信號的中心頻率。

式中:Ａ 為參考信號的幅值下標 ｉ 代表應答器的 身份編號ｉ ＝ １、２、３

基陣接收的每一路信號都要通過３路并聯的Ｎｏｔｃｈ濾波器，選擇合適的自適應算法，通過濾波器的輸出結果就可以檢測出發送該信號所對應的 應答器，然后通過相位差估計器解算出該信號在基陣相鄰陣元間的相位差。

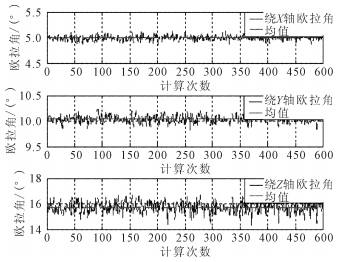
式中:下標 ｉ 代表應答器的身份ｍ、ｎ代表基陣中相鄰的陣元

２ 仿真計算

      通過仿真計算來驗證ＵＳＢＬ對應答器進行定位解算待沉管節平面位姿的有效性，仿真中ＵＳＢＬ定位系統測時誤差取值為０. １ ｍｓ定位精度誤差取值為０. １％ 斜距待沉管節上安裝有３個不共線的應答器，組成一個直角三角形，管節平面相對于ＵＳＢＬ基陣坐標的歐拉旋轉角度設置為θｘ ＝ ５°，θｙ ＝ １０°，θｚ ＝ １５°。

      通過上述位姿解算方法，求解出待沉管節平面相對于ＵＳＢＬ基陣的歐拉角:θｘ＝ 4.95°，θｙ ＝ 10.04°，其中繞,Ｚ軸的歐拉角出現無解狀態，這是由于方向余弦矩陣有 ９ 個分量，實際只有３個自由度，假設歐拉角為未知量，通過法向量直接求解方向余弦矩陣，則使得矩陣為非滿秩陣，從而出現繞Ｚ軸歐拉角度無解的狀態，為此，配合應答器初始位置并通過已解算出來的 θｘ、θｙ 值再解算繞Ｚ軸的歐拉角，最終得到管節平面繞 Ｚ 軸旋轉的歐拉角，仿真求解的歐拉角均值:θｘ ＝５. ００１ ４°，θｙ ＝ １０. ０３８°，θｚ ＝ １５. ７８°，計算誤差:Δθｘ ＝ ０. ０１°， Δθｙ ＝ ０. ０２°，Δθｚ ＝ ０. ０３°，見圖 ３

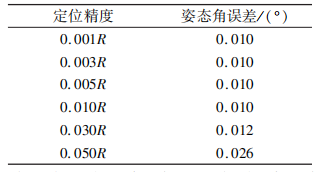
圖 ３ 管節平面位姿角度仿真計算結果(基陣坐標系)

２. １ 姿態角估計精度

管節姿態角估計精度與超短基線定位精度有直接關系，因此仿真驗算了定位精度和姿態角估 計精度之間的關系，仿真步驟:沉管在大地坐標系下的歐拉角精確值為[５° １０° １５°]，改變超短 基線定位系統的定位精度，求姿態角的誤差，以繞 Ｘ 軸姿態角誤差為例ꎬ結果見表１

表 １ ＵＳＢＬ 定位精度與繞 Ｘ 軸歐拉角的關系

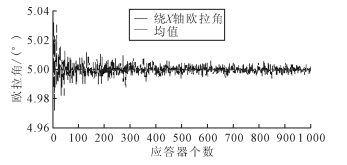
表 １ 中 Ｒ 為基陣坐標系原點到局部坐標系 原點的斜距， 由表 １ 可見，超短基線定位精度由 ０. ０５０Ｒ 增加到 ０. ００１Ｒ 時，回收平臺姿態角度誤 差也就越來越小，在水文環境較好的背景下，基 于Ｎｏｔｃｈ濾波器的超短基線定位系統的精度高于０. ０１０Ｒ時，此時姿態角誤差達到了 ０. ０１０°，可以 滿足工程需要２. ２ 沉管表面

２. ２ 沉管表面應答器個數

       理論上 ３ 個應答器即可決定沉管的定位面，且應答器個數越多，冗余信息量增加，參數估計的 精度有相應提高，但應答器個數太多，會增加成本和計算復雜度，為了研究應答器個數和姿態角估計精度之間的關系，進行了如下仿真計算:改變 應答器的個數，對每個應答器的位置進行解算，每增加一個應答器，就利用新的冗余信息對前一 次計算的歐拉角進行修正，求解管節平面的姿態 角(以繞 Ｘ 軸歐拉角為例)見圖 ４

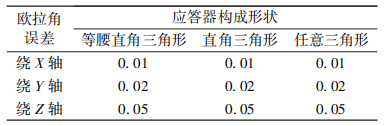
圖 ４ 管節平面安裝應答器個數與姿態角度 (繞 Ｘ 軸)誤差的關系

圖 ４ 表明當應答器個數從3增至 1000個姿態角估計精度也逐漸提高，但精度的提高僅在,極小的量級，最高不超過 0.020°，不符合工程實,際，并且由仿真可知，當定位精度高于0.010Ｒ 時，安裝,３個應答器的角度估計誤差便小于 0.010°.    

表 ２ 應答器構成形狀與姿態角估計的關系 (°)

由表 ２ 可見應答器的布放形式對姿態估計精度沒有影響，這一結論使得應答器在沉管上的安裝變得更為方便，可以根據施工要求靈活選取，避開高噪聲區，同時，可將應答器安裝在ＵＳＢＬ定位精度較高的基陣正下方，有助于提高位姿算法的精度。

３ 結論

       相比于單一的傳統沉管下沉測控方法，本文 提出基于ＵＳＢＬ定位系統的管節沉放測控方案，在管節下沉階段可輔助待沉管節較為精確地布放到待沉區域(粗測階段)，而后結合高精度相對法完成最終的對接定位過程(精測階段)，該方案的優勢如下。

１)滿足遠岸、深水的沉管施工要求，超短基線聲學定位系統不依靠岸基上的輔助設施，擺脫 了離岸距離的限制，同時，與傳統定位方法相比，在深水區依然滿足施工精度，與ＧＰＳ系統結合后，可以實時顯示沉管在大地坐標中的三維姿態參數，可有效輔助遠岸、深水環境下的沉管水下沉放施工。

２)設備成本低，安裝方便，作業安全性高，超短基線聲學定位系統體積小、成本低廉，作業 前只需要在沉管上表面按需求安裝３個應答器，無需安裝測量塔，安裝過程在水面進行，可減少施 工人員下水作業次數，整個施工過程效率高、安全性高、操作復雜性低。

參考文獻 

[１] 王解先 許琛 陸彩萍. 沉管沉放的實時監測[ Ｊ]. 測 繪學報 ２００２ ３１(增刊 １):７０￣７２. 

[２] 范東明 路伯祥. ＧＰＳ 隧道平面控制測量中若干問題 研究[Ｊ]. 解放軍測繪學院學報 １９９８(１):１７￣２０. 

[３] 鎖旭宏. 組合式測控技術在外海超長沉管隧道安裝 中的應用[Ｊ]. 公路 ２０１８(８):３７￣４２. 

[４] 張彥昌 黃永軍. 港珠澳大橋隧道沉管安裝定位及姿 態監測技術[Ｊ]. 海洋測繪 ２０１２ ３２(５):２５￣２８. 

[５] 任朝軍 蘇林王 呂黃 等. 聲納法在管節沉放實時定 位測量中的應用[ Ｊ]. 現代隧道技術 ２０１２ ４９ (５): １３２￣１３６. 

[６] 任朝軍 呂黃 蘇林王 等. 沉管隧道管節沉放實時定 位測量技術現狀分析[ Ｊ]. 現代隧道技術 ２０１２ ４９ (１):４４￣４９.

班寧產品匯總